IRIS SCANNING (Seminar report)
INTRODUCTION
The iris is an externally visible, yet protected organ whose unique epigenetic pattern remains stable throughout adult life. These characteristics make it very attractive for use as a biometric for identifying individuals. The purpose of ‘Iris Recognition’, a biometrically based technology for personal identification and verification, is to recognize a person from his/her iris prints. In fact, iris patterns are characterized by a high level of stability and distinctiveness. Each individual has a unique iris. The difference even exists between identical twins and between the left and right eyes of the same person.
The probability of finding two people with identical iris patterns is considered to be approximately 1 in 1052(the population of the earth is of the order 1010). Not even one-legged twins or a future clone of a person will have the same iris patterns. The iris is considered to be an internal organ because it is so well protected by the eyelid and the cornea from environmental damage. Iris recognition is the most precise and fastest biometric authentication method.
Table1.1: COMPARISION OF MAJOR BIOMETRIC TECHNIQUES
HUMAN IRIS:
The iris is a thin circular diaphragm, which lies between the cornea and the lens of the human eye. A front-on view of the iris is shown in Figure 2.1. The iris is perforated close to its center by a circular aperture known as the pupil. The function of the iris is to control the amount of light entering through the pupil, and this is done by the sphincter and the dilator muscles, which adjust the size of the pupil. The average diameter of the iris is 12 mm, and the pupil size can vary from 10% to 80% of the iris diameter.
The iris consists of several layers; the lowest in the epithelium layer, which contains dense pigmentation cells. The stromal layer lies above the epithelium layer and contains blood vessels, pigment cells, and the two iris muscles. The density of stromal pigmentation determines the color of the iris.
The externally visible surface of the multi-layered iris contains two zones, which often differ in color. An outer ciliary zone and an inner pupillary zone, and these two zones are divided by the collarette – which appears as a zigzag pattern
WORKING OF IRIS RECOGNITION SYSTEM:
Image processing techniques can be employed to extract the unique iris pattern from a digitized image of the eye, and encode it into a biometric template, which can be stored in a database. This biometric template contains an objective mathematical representation of the unique information stored in the iris and allows comparisons to be made between templates. When a subject wishes to be identified by the iris recognition system, their eye is first photographed, and then a template is created for their iris region. This template is then compared with the other templates stored in a database until either a matching template is found and the subject is identified, or no match is found and the subject remains unidentified.
Fig 2.1 HUMAN EYE
FEATURES OF IRIS RECOGNITION:
- Measurable Physical Features: 250 degrees of freedom,250 non-related unique features of a person’s iris
- Unique: Every iris is absolutely unique. No two iris are the same
- Stable: iris remains stable from 1styear till death.
- Accurate: Iris recognition is the most accurate of the commonly used biometric technologies.
- Fast: Iris recognition takes less than 2 seconds. 20 times more matches per minute than its closest competitor.
- Non-Invasive: No bright lights or lasers are used in the imaging and iris authentication process.
IRIS RECOGNITION SYSTEM STRENGTHS:
- Highly Protected: Internal organ of the eye. Externally visible; patterns imaged from a distance
- Measurable Features of iris pattern: Iris patterns possess a high degree of randomness
- Variability: 244 degrees-of-freedom
- Entropy: 3.2 bits per square-millimeter
- Uniqueness: Set by combinatorial complexity
- Stable: Patterns apparently stable throughout life
- Quick and accurate: Encoding and decision-making are tractable Image analysis and encoding time: 1 second
IRIS RECOGNITION SYSTEM WEAKNESS:
- Some difficulty in usage as individuals doesn’t know exactly where they should position themselves.
- And if the person to be identified is not cooperating by holding the head still and looking into the camera.
IRIS SYSTEM IMPLEMENTATION
IMAGE ACQUISITION:
Image acquisition is considered the most critical step in the project since all subsequent stages depend highly on the image quality. To accomplish this, we use a CCD camera. We set the resolution to 640x480, the type of the image to jpeg, and the mode to white and black for greater details. The camera is situated normally between half a meter to one meter from the subject. (3 to 10 inches)
The CCD-cameras job is to take the image from the optical system and convert it into electronic data. Find the iris image by a monochrome CCD (Charged Couple Device) camera transfer the value of the different pixels out of the CCD chip. Read out the voltages from the CCD chip. Thereafter the signals of each data are amplified and sent to an ADC (Analog to Digital Converter).
Figs 2.1 BLOCK DIAGRAM OF IMAGE ACQUISITION USING CCD CAMERA
IMAGE MANIPULATION:
In the preprocessing stage, we transformed the images from RGB to gray level and from eight-bit to double-precision thus facilitating the manipulation of the images in subsequent steps.
IRIS LOCALIZATION:
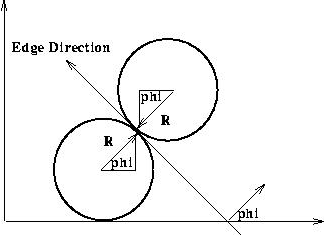
Before performing iris pattern matching, the boundaries of the iris should be located. In other words, we are supposed to detect the part of the image that extends from inside the limbus (the border between the sclera and the iris) to the outside of the pupil. We start by determining the outer edge by first downsampling the images by a factor of 4 then use the canny operator with the default threshold value given by Matlab, to obtain the gradient image.
Since the picture was acquired using an infrared camera the pupil is a very distinct black circle. The pupil is in fact so black relative to everything else in the picture simple edge detection should be able to find its outside edge very easily. Furthermore, the thresholding on the edge detection can be set very high as to ignore smaller less contrasting edges while still being able to retrieve the entire perimeter of the pupil. The best edge detection algorithm for outlining the pupil is canny edge detection. This algorithm uses horizontal and vertical gradients in order to deduce edges in the image. After running the canny edge detection on the image a circle is clearly present along the pupil boundary.
Canny Edge Detector finds edges by looking for the local maxima of the gradient of the input image. It calculates the gradient using the derivative of the Gaussian filter. The Canny method uses two thresholds to detect strong and weak edges. It includes the weak edges in the output only if they are connected to strong edges. As a result, the method is more robust to noise and more likely to detect true weak edges.
EDGE DETECTION:
Edges often occur at points where there is a large variation in the luminance values in an image, and consequently, they often indicate the edges, or occluding boundaries, of the objects in a scene. However, large luminance changes can also correspond to surface markings on objects. Points of tangent discontinuity in the luminance signal can also signal an object boundary in the scene.
So the first problem encountered with modeling this biological process is that of defining, precisely, what an edge might be. The usual approach is to simply define edges as step discontinuities in the image signal. The method of localizing these discontinuities often then becomes one of finding local maxima in the derivative of the signal or zero-crossings in the second derivative of the signal.
In computer vision, edge detection is traditionally implemented by convolving the signal with some form of linear filter, usually a filter that approximates a first or second derivative operator. An odd symmetric filter will approximate the first derivative, and peaks in the convolution output will correspond to edges (luminance discontinuities) in the image.
An even symmetric filter will approximate a second derivative operator. Zero-crossings in the output of convolution with an even symmetric filter will correspond to edges; maxima in the output of this operator will correspond to tangent discontinuities, often referred to as bars or lines.
CANNY EDGE DETECTOR:
Edges characterize boundaries and are therefore a problem of fundamental importance in image processing. Edges in images are areas with strong intensity contrasts
– a jump in intensity from one pixel to the next. The edge detecting an image significantly reduces the amount of data and filters out useless information while preserving the important structural properties in an image.
The Canny edge detection algorithm is known to many as the optimal edge detector. A list of criteria to improve current methods of edge detection is the first and most obvious is the low error rate. It is important that edges occurring in images should not be missed and that there be NO responses to non-edges. The second criterion is that the edge points be well localized. In other words, the distance between the edge pixels as found by the detector and the actual edge is to be at a minimum. A third criterion is to have only one response to a single edge. This was implemented because the first 2 were not substantial enough to completely eliminate the possibility of multiple responses to an edge.
The Process of the Canny edge detection algorithm can be broken down into 5 different steps:
Apply Gaussian filter to smooth the image in order to remove the noise
Find the intensity gradients of the image
Apply non-maximum suppression to get rid of spurious response to edge detection
Apply double threshold to determine potential edges
Track edge by hysteresis: Finalize the detection of edges by suppressing all the other edges that are weak and not connected to strong edges.
HOUGH TRANSFORM:
The Hough transform is a technique that can be used to isolate features of a particular shape within an image. Because it requires that the desired features be specified in some parametric form, the classical Hough transform is most commonly used for the detection of regular curves such as lines, circles, ellipses, etc. A generalized Hough transform can be employed in applications where a simple analytic description of a feature(s) is not possible. Due to the computational complexity of the generalized Hough algorithm, we restrict the main focus of this discussion to the classical Hough transform.
Despite its domain restrictions, the classical Hough transform (hereafter referred to without the classical prefix) retains many applications; as most manufactured parts contain feature boundaries that can be described by regular curves. The main advantage of the Hough transform technique is that it is tolerant of gaps in feature boundary descriptions and is relatively unaffected by image noise.
The Hough transform is computed by taking the gradient of the original image and accumulating each non-zero point from the gradient image into every point that is one radius distance away from it.
That way, edge points that lie along the outline of a circle of the given radius all contribute to the transform at the center of the circle, and so peaks in the transformed image correspond to the centers of circular features of the given size in the original image. Once a peak is detected and a circle 'found' at a particular point, nearby points (within one-half of the original radius) are excluded as possible circle centers to avoid detecting the same circular feature repeatedly.
Hough circle detection with gradient information.
One way of reducing the computation required to perform the Hough transform is to make use of gradient information which is often available as output from an edge detector. In the case of the Hough circle detector, the edge gradient tells us in which direction a circle must lie from a given edge coordinate point.
The Hough transform can be seen as an efficient implementation of a generalized matched filter strategy. In other words, if we created a template composed of a circle of 1's (at a fixed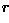 
) and 0's everywhere else in the image, then we could convolve it with the gradient image to yield an accumulator array-like description of all the circles of radius 
in the image. Show formally that the basic Hough transforms (i.e. the algorithm with no use of gradient direction information) is equivalent to template matching.
) and 0's everywhere else in the image, then we could convolve it with the gradient image to yield an accumulator array-like description of all the circles of radius 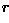in the image. Show formally that the basic Hough transforms (i.e. the algorithm with no use of gradient direction information) is equivalent to template matching.
EDGE MAPS:
1) an eye image 2) corresponding edge map 3) edge map with only horizontal gradients 4) edge map with only vertical gradients.
Iris recognition technology converts the visible characteristics of the iris into a 512 byte Iris Code, a template stored for future verification attempts. 5l2 bytes is a fairly compact size for a biometric template, but the quantity of information derived from the iris is massive. From the iris 11 mm diameters, Dr. Daugman’s algorithms provide 3.4 bits of data per square mm. This density of information is such that each iris can be said to have 266 unique “spots”, as opposed to 13- 60 for traditional biometric technology. This 266 measurement is cited in all iris recognition literature, after allowing for the algorithms for relative functions and for characteristics inherent to most human eyes. Dr. Daugman concludes that 173 “independent binary degrees of freedom can be extracted from his algorithm-and exceptionally large number fur a biometric, for future identification, the database will not be comparing images of iris, but rather hexadecimal representations of data returned by wavelet filtering and mapping. The Iris Code for an iris is generated within one second. Iris Code record is immediately encrypted and cannot be reverse-engineered.
Iris code
Pattern matching:
When a live iris is presented for comparison, the iris pattern is processed and encoded into 512 bytes Iris Code. The Iris Code derived from this process is compared with the previously generated Iris Code. This process is called pattern matching. Pattern matching evaluates the goodness of match between the newly acquired iris pattern and the candidate’s database entry. Based on this goodness of match final decision is taken whether acquired data does or doesn’t come from the same iris as does the database entry.
Pattern matching is performed as follows. Using integer XOR logic in a single clock cycle, a long vector of each to iris code can be XORed to generate a new integer. Each of whose bits represents a mismatch between the vectors being compared. The total number of 1s represents the total number of mismatches between the two binary codes. The difference between the two recodes is expressed as a fraction of mismatched bits termed as hamming distance. For two identical Iris Codes, the hamming distance is Zero. For perfectly unmatched Iris Codes, the hamming distance is 1. Thus iris patterns are compared. The entire process i.e. recognition process takes about 2 seconds. A key differentiator for iris recognition is its ability to perform identification using a one-to-many search of a database, with no limitation on the number of iris code records contained therein.
Accuracy:
The Iris Code constructed from these Complex measurements provides such a tremendous wealth of data that iris recognition offers a level of accuracy orders of magnitude higher than biometrics. Some statistical representations of the accuracy follow:- The odds of two different irises returning a 75% match (i.e. having Hamming Distance of 0.25): 1 in 10 16.
- Equal Error Rate (the point at which the likelihood of a false accept and false reject are the same): 1 in 12 million.
Other numerical derivations demonstrate the unique robustness of these algorithms. A person’s right and left eyes have a statistically insignificant increase in similarity: 0.0048 on a 0.5 mean. This serves to demonstrate the hypothesis that iris shape and characteristics are phenotypes - not entirely; determined by the genetic structure. The algorithm can also account for the iris: even if 2/3 of the iris were completely obscured, an accurate measure of the remaining third would result in an equal error rate of 1 in 100000.
Comparison between genetically identical iris patterns:
Although the striking visual similarity of identical twins reveals the genetic penetrance of overall facial appearance, a comparison of genetically identical irises reveals just the opposite for iris patterns: the iris texture is an epigenetic phenotypic feature, not a genotypic feature. A convenient source of genetically identical irises are the right and left pair from any given person. Such pairs have the same genetic relationship as the four irises of two identical twins, or indeed in the probable future, the 2N irises of N human clones. The eye color of course has high genetic penetrance, as does the overall statistical quality of the iris texture, but the textural details are uncorrelated and independent even in genetically identical pairs. So performance is not limited by the birth rate of identical twins or the existence of genetic relationships.
Advantages
Highly protected, internal organ of the eye
Externally visible; patterns imaged from a distance
Iris patterns possess a high degree of randomness
o Variability: 244 degrees-of-freedom
o Entropy: 3.2 bits per square-millimeter
o Uniqueness: set by combinatorial complexity
Changing pupil size confirms natural physiology
Pre-natal morphogenesis (7th month of gestation)
Limited genetic penetrance of iris patterns
Patterns apparently stable throughout life
Encoding and decision-making are tractable
Image analysis and encoding time: 1 second
Decidability index (d-prime): d' = 7.3 to 11.4
Search speed: 100,000 Iris Codes per second
Disadvantages of using iris for identification
Small target (1 cm) to acquire from a distance (1m)
Located behind a curved, wet, reflecting surface
Obscured by eyelashes, lenses, reflections
Partially occluded by eyelids, often drooping
Deforms non-elastically as pupil changes size
Illumination should not be visible or bright
Some negative connotations
Applications
Iris-based identification and verification technology have gained acceptance in a number of different areas. The application of iris recognition technology can be limited only by imagination. The important applications are those following:
- ATM’s and iris recognition: in the U.S many banks incorporated iris recognition technology into ATMs for the purpose of controlling access to one’s bank accounts. After enrolling once (a “30 second” process), the customer need only approach the ATM, follow the instruction to look at the camera, and be recognized within 2-4 seconds. The benefits of such a system are that the customer who chooses to use the bank’s ATM with iris recognition will have a quicker, more secure transaction.
- Tracking Prisoner Movement: The exceptionally high levels of accuracy provided by iris recognition technology broadens its applicability in high-risk, high-security installations. Iris scan has implemented its devices with great success in prisons in Pennsylvania and Florida. By this, any prison transfer or release is authorized through biometric identification. Such devices greatly ease logistical and staffing problems.
Applications of this type are well suited to iris recognition technology. First, being fairly large, iris recognition physical security devices are easily integrated into the mountable, sturdy apparatuses needed for access control, The technology’s phenomenal accuracy can be relied upon to prevent the unauthorized release or transfer and to identify repeat offenders re-entering prison under a different identity.
Computer login: The iris as a living password.
National Border Controls: The iris as a living password.
Telephone call charging without cash, cards, or PIN numbers.
Ticketless air travel.
Premises access control (home, office, laboratory, etc.).
Driving licenses and other personal certificates.
Entitlements and benefits authentication.
Forensics, birth certificates, tracking missing or wanted person
Credit-card authentication.
Automobile ignition and unlocking; anti-theft devices.
Anti-terrorism (e.g.:— suspect Screening at airports)
Secure financial transactions (e-commerce, banking).
Internet security, control of access to privileged information.
“Biometric—Key Cryptography “for encrypting/decrypting messages.
CONCLUSION
The technical performance capability of the iris recognition process far surpasses that of any biometric technology now available. The iridian process is defined for a rapid exhaustive search for very large databases: distinctive capability required for authentication today. The extremely low probabilities of getting a false match enable the iris recognition algorithms to search through extremely large databases, even of a national or planetary scale. As iris technology grows less expensive, it could very likely unseat a large portion of the biometric industry, e-commerce included; its technological superiority has already allowed it to make significant inroads into identification and security venues which had been dominated by other biometrics. Iris-based biometric technology has always been an exceptionally accurate one, and it may soon grow much more prominent.
0 Comments